如何识别低对比度露珠？

更新AIGC结果

评论区的大家觉得要么一张图的测试结果太少了，要么是建议用语义分割来做会更好，但这些建议都会遇到一个新的难题：目前只有一张图怎么办？

不巧这恰恰刚好是实际的工业场景中经常遇到的情况，不管是因为这个缺陷过于稀有，还是因为目前工厂流水线还没有开始正常跑料，甚至还可能是这个料太贵了不能人造缺陷来采图（比如一颗GPU芯片），实际会遇到各种各样的原因导致我们在项目的某个阶段只能拿到极为稀少的样本的情况。在过去的10年里，我做过的项目中，遇到的这种情况是非常多的。

针对这个问题，我觉得更好的解决方案是AIGC技术。我用我们团队开发的算法测试了一下案例中的这一张图，分两步来生成样本图片。

第一步：生成更加多样化的背景

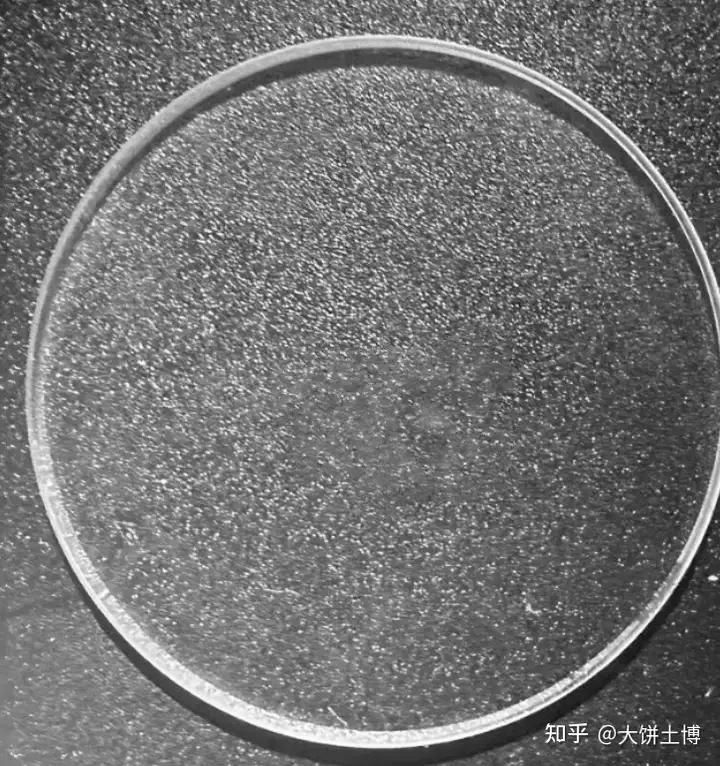
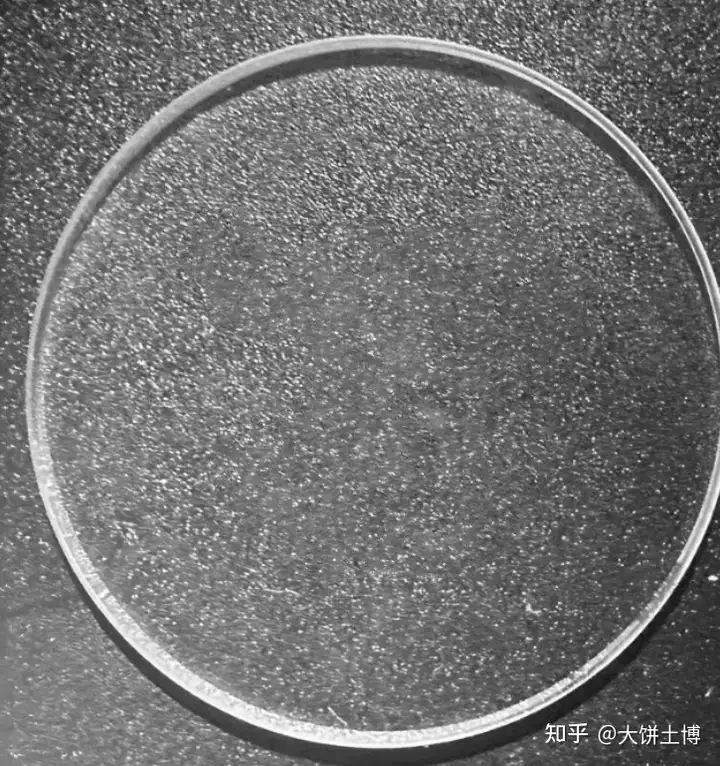
第二步，往这些自动生成的背景图上生成缺陷

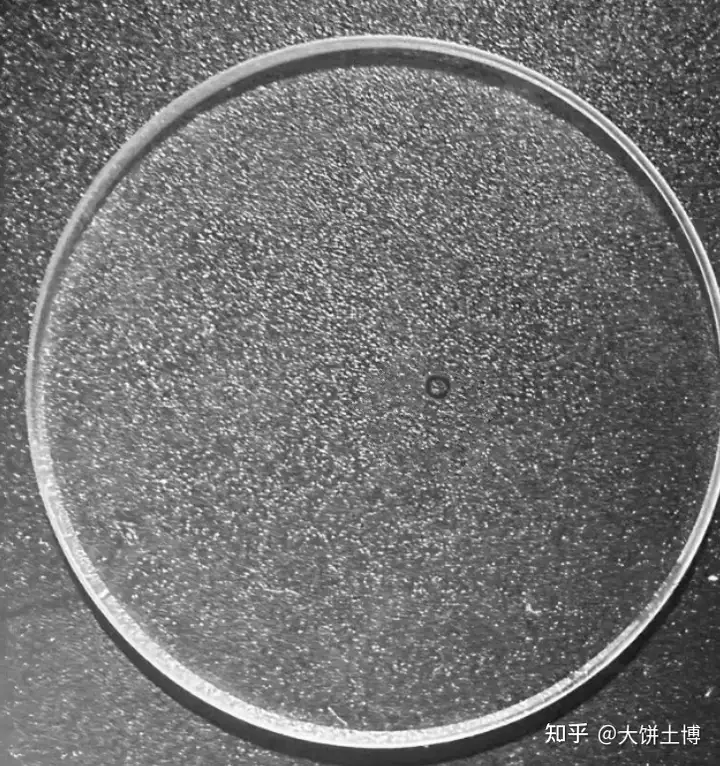
为方便大家观看，下面我把部分生成的缺陷从大图里裁剪出来

我相信，基于这些自动生成的样本，训练一个模型去检测应该不难，上个yolo足够了。虽然讨论到这里，似乎有点偏离这个原本的问题了，但我还是想贴这些图出来，和同行们交流看看，这个自动生成图片来训练模型的路子，大家是怎么看的。

原答案

从这个图片看，露珠在图像上看的外观特征主要是：

形状接近圆形

边缘存在一圈黑边

直接基于这两个特征的描述，第一个最简单的思路就是：用斑点分析算法对所有偏黑的斑点，基于圆度属性过滤，得到接近圆形的斑点，即为此露珠。

下面我们一步步来看。输入图像先被转换成了灰度图，斑点分析所使用的灰度范围设定为0~70，此时得到的阈值分割结果如下图所示

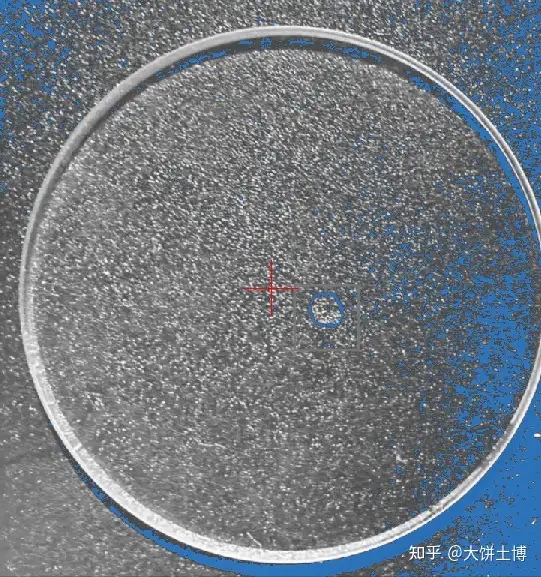
可以看到因为亮度不均匀，有很多干扰的斑点检出，但后续我们还可以设定圆度，所以这里并不是大问题。放大要检测的露珠部分如下图所示

可以发现斑点的轮廓因为亮度不均匀而断开了，所以很自然可以想到这里可以用形态学算法来补上这个缺口，使用形态学开操作（3*3的矩形核）之后如下图

可以看到斑点正常连接好了。此时我猜测这个斑点的圆度应该大于0.5了，所以设定了圆度范围0.5~1来过滤所有斑点，同时设定了面积的范围是大于100来过滤掉很小的斑点，结果如下图所示

此时发现多检出了一个小斑点在右下角，放大看如下

同时，查看露珠斑点和这个小斑点的圆度数值分别为0.7和0.527，由此，可修改圆度值的过滤范围为0.6~1，即可得到仅有一个露珠的过滤结果。最终结果如下图所示

以上为针对这个图片的最简单的方法。调用opencv的python代码如下：

import cv2
import numpy as np

# 1. 从文件读取图像
img = cv2.imread('test.png')
if img is None:

print("无法加载图像 test.png")

exit()

# 2. 将图像转换成灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 3. 使用kernel形状是3*3的正方形的形态学开操作处理图像
kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
img_opened = cv2.morphologyEx(gray, cv2.MORPH_OPEN, kernel)

# 4. 对处理后的图像使用阈值处理，确保灰度范围为0~70
_, img_thresh = cv2.threshold(img_opened, 70, 255, cv2.THRESH_BINARY_INV)

# 5. 使用findContours方法找到所有轮廓
contours, _ = cv2.findContours(img_thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

# 6. 筛选出满足条件的斑点（圆度取值范围为0.6~1）
for cnt in contours:

# 计算轮廓的面积和周长

area = cv2.contourArea(cnt)

if area < 100:

continue

perimeter = cv2.arcLength(cnt, True)

if perimeter == 0:

continue

# 防止除以零错误

# 计算圆度（Circularity），公式：4*pi*area/perimeter^2

circularity = 4 * np.pi * area / (perimeter ** 2)

# 如果圆度在0.6到1之间，则认为该轮廓是有效的斑点

if 0.5 <= circularity <= 1:

print(f'{cnt}: circularity {circularity:.3f}')

# 绘制轮廓线，颜色为白色(255,255,255)，线宽为2

cv2.drawContours(img, [cnt], -1, (255, 255, 255), 2)

# 显示结果
cv2.imshow('Detected Blobs', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

# 保存结果图像
cv2.imwrite('output_blobs.png', img)

虽然以上思路对这张图可以得到正确的结果，但不代表这个思路是最好的，通常我们还得提前考虑实际生产环境中采集到的图片的多样性，尽量让算法的抗干扰能力更强。

重新审视一下原图，可以发现整体亮度不均匀现象还是很明显的，这让0~70这个灰度范围的设定存在不适用未来的实际图片的风险，所以，可以考虑用常见的对抗亮度不均匀的图像处理算法来做预处理先，例如基于自适应阈值的方法

以上动图展示的是逐步调节自适应阈值的C参数的逐帧变化效果，最终可以看到分割结果也是成功的，python代码段也很简单，对上面代码中的img_opened使用如下代码处理，将C从0开始逐步+1增加即可得到以上动画中的二值图的演变过程

img_thresh = cv2.adaptiveThreshold(img_opened, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY_INV, blockSize=31, C=0)

除以上行业里经常用的经典思路外，还可以尝试一下频域图像处理的思路，得到如下所示结果

先使用经典的二维快速傅里叶变换转换到频谱图，再用带通滤波器（带宽20，径向中心频率36）得到以上右侧的滤波后的频谱图（显示的幅值图），最后重建回空域得到了以上右侧的图像，可以看到左侧图像中的露珠所处位置出现一个黑点。为更直观地观察带通滤波器的效果，可以看以下动图

在以上动图中，我把带宽固定成了20，连续改变径向中心频率从0到60，基于这个效果，我得到了最优径向中心频率36，代码如下

import numpy as np
import cv2

def ideal_bandpass_mask(shape, center_frequency, bandwidth):

"""生成理想带通滤波器的掩模"""

mask = np.zeros(shape)

rows, cols = shape

crow, ccol = rows//2 , cols//2

radialCen2 = center_frequency * center_frequency

bandWidth2 = bandwidth * bandwidth

# 创建频率范围矩阵

rc2 = (np.linspace(-crow, crow, rows))[:, np.newaxis] ** 2 + (np.linspace(-ccol, ccol, cols)) ** 2

coef = np.pow(rc2 - radialCen2, 2) / bandWidth2 / (rc2 + np.finfo(np.float32).eps)

return np.exp(-np.pow(coef, 2))

# 读取图像并转换为灰度图像
img = cv2.imread('test.png', 0)

# 傅里叶变换
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

# 获取形状参数
rows, cols = img.shape
mask = ideal_bandpass_mask((rows, cols), 36, 20)

# 确保掩模是双通道的，与DFT结果相匹配
mask_complex = mask.astype(np.float32) + 1j * mask.astype(np.float32)
mask_complex = np.stack([mask_complex.real, mask_complex.imag], axis=-1)

# 应用带通滤波器
dft_shift_filtered = cv2.mulSpectrums(dft_shift, mask_complex, cv2.DFT_ROWS)

# 逆傅里叶变换
f_ishift = np.fft.ifftshift(dft_shift_filtered)
img_back = cv2.idft(f_ishift)
img_back_real = img_back[:, :, 0]

# 转换频谱图为可视格式
dft_shift_filtered_mag = cv2.magnitude(dft_shift_filtered[:,:,0], dft_shift_filtered[:,:,1])

# 显示结果
import matplotlib.pyplot as plt

# 显示结果
plt.figure(figsize=(20, 10))
plt.subplot(131), plt.imshow(img_back_real, cmap='gray')
plt.title('Reconstructed Image'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(dft_shift_filtered_mag, cmap='gray')
plt.title('Filtered Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(mask, cmap='gray')
plt.title('Bandpass Filter Mask'), plt.xticks([]), plt.yticks([])
plt.show()

备注：以上截图及动画均来自利珀开发的IntelliBlink视觉开发平台软件，和python代码运行结果在展示效果上存在不同，但算法的结果是一致的。