如题
2 Answers
图像傅立叶变换是一个重要的图像处理算法,但它比一般的算法都更难理解和使用。许多资料都喜欢从公式和原理出发来解释,但这样解释还是很难让大家很快了解它应该怎么用。
我相信,学习一个新的算法,并不总是需要从原理开始的。
从原理开始的学习方法,适合某些人,但并不适合所有人。
先看看这个算法能用来做什么,喂给它一些不同的输入,先看看它会有哪些输出,由此先构建好对它的直观认识,也是一种很好的学习方法。
这样做了以后,你会在脑中构建出一种朴素的对它背后的原理的一种推断,之后,如果你再去读它的原理,理解就会更深刻。
下面,我就分享一下我当时学习图像傅里叶变换时做的实验。
从我当年面试被问的那个问题开始,我在黑色画布中心画了一个白点(1x1像素)

它的频谱图(取对数后,下同)是

虽然一个点很小,但它的频谱却像个中间微微凸起的方块面包。
我把点弄大了点(3x3像素)

它的频谱图是

有点意思。
那再弄大点看看(21x21像素)

它的频谱图是

看起来的规律是,正方形的点慢慢变大的时候,频谱图上的方格会变小变多变密。
那如果是圆点的话,频谱图会有什么不一样?
半径5像素的圆如下

它的频谱图是

如果圆更大点(半径11像素)

它的频谱图是

规律和小方块类似!也是它自己越大的时候,频谱图上的圆就会越密。不过也有异常的现象,就是外圈似乎变得很奇怪。放大原图(半径5像素的圆)可以看到,用像素绘制的圆其实没那么“圆”

好了,这是两种形状的点和不同大小的时候的现象。下面来看看线。
这是一条横线和它的频谱图(左图是原图,右图是频谱图,下同)

Amazing!横线的频谱图居然是竖线!那我猜竖线的频谱图就是横线

果然如此。
那如果是很多平行线呢?


从这两个图的频谱,可以推断出:平行线的频谱是等间距分布在原图平行线的一条垂线上的点。
我们现在已经看过单条的线和平行线的频谱图了,那前面的圆,对应的应该就是圆环了

前面这些实验,一个图中只用了相邻之间等间距的几何对象,那如果把两种方向的几何对象组合在一起呢?比如两个方向的平行线组合在一起,就得到了网格

网格线的频谱图是等间距均匀分布的网格点。
前面的那个长得比较奇怪的圆频谱图还让我有点耿耿于怀,所以我尝试绘制了亮度呈正弦分布的圆环

所以,正弦分布的圆环的频谱图,其实是一个圆,圆的半径和正弦分布的频率似乎存在正比关系。
做了这么多实验有什么用呢?总结上面这些图的规律,我们是不是发现,平行线、等间距圆环和网格线这些图形都存在一个共性,那就是“重复”。这些图形中存在许多重复出现的模式,这些模式在频谱图上总是表现为一些局部来看比较亮的小点或细线。它们和单一的方形或圆形的频谱图明显不同,没有出现大片的比较亮的区域。
现在我们可以合理推断,重复出现的模式在频谱图上会表现为比较细小的亮点或亮线。
那么,如果我修改频谱图,把频谱图中的这些细小的亮点和亮点的灰度值改为0,是不是就能消除原图中对应的重复模式呢?
比如我们现在已经知道网格线对应的频谱图是等间距的网格点,如果这些点被消除了,那原图中的网格线也应该被消除。正弦分布的圆环的实验中,频谱图上的圆如果被消除了,那原图中的圆环图案应该也会消除。
下面我们来一个接近真实的样例图,芯片阵列

芯片阵列的图像处理过程上面的6个图是我设计的简单的频域处理流程得到的step-by-step的结果图,从左到右,从上到下依次是
- 原始芯片阵列照片
- 原始照片的频谱图
- 为消除频谱图上的亮点而得到遮罩(mask)图
- 将遮罩图应用于频谱图得到的“滤波”结果
- 将“滤波”结果重建回空域图,即被消除了芯片图案之后的照片。
从这个流程的结果可以看出,通过我们对频谱图的处理,最终第5步重建的灰度图中确实就看不到芯片的图案了。
那么,为什么我们需要消除重复的芯片图案呢?
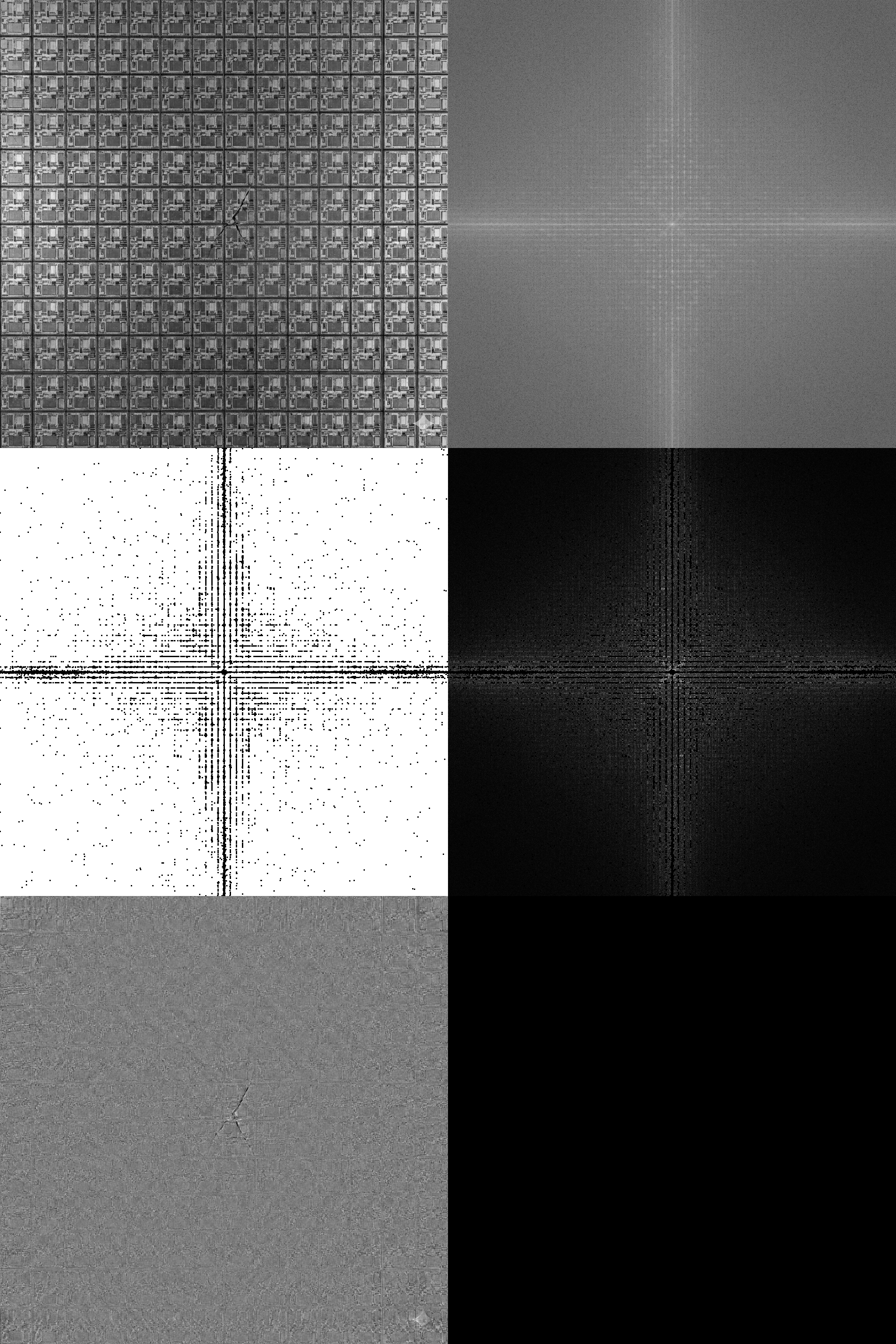
有缺陷的芯片阵列的图像处理过程这张裂纹图的处理结果就是一个典型的缺陷检测项目中可能会用的预处理结果了。通过这样的预处理,我们就可以把缺陷凸显出来,后续检测裂纹,就可以用比较简单的算法来进行了。